C++ code common algorithms

Posted on | In
| Words count in article 1016

C++ code common algorithms

Dijkstra

Assume N nodes, source node is indexed by root, using adjacency list

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<climits> // INT_MAX
#include<vector>
#include<queue> // priority_queue
#include<<utility>> // pair
typedef pair<int, int> pii; // weight goes first 

vector<int> dist(N, INT_MAX);
dist[root] = 0;
priority_queue<pii, vector<pii>, greater<pii>> q;
q.push(make_pair(0, root));
while(!q.empty()){
  pii current = q.top();
  q.pop();
  for(pii neighbor : adj[current.second]){
    if(dist[neighbor.second] > dist[current.second] + neighbor.first){
      dist[neighbor.second] = dist[current.second] + neighbor.first;
      q.push(make_pair(dist[neighbor.second], neighbor.second));
    }
}

To track the actual shortest path, introduce an array int Predecessor[N], update whenever dist[neighbor.second] changes, simply set to the new predecessor current.second.

Union Find

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<map>
#include<<utility>> // pair

map<int, pair<int, int>> m; // map to parent & rank

void makeSet(int x, map<int, pair<int, int>>& m){
  m.insert(make_pair(x, make_pair(x, 0)));
}
    
int findSet(int x, map<int, pair<int, int>>& m){
  if(m[x].first == x) return x;
  else{
    m[x].first = findSet(m[x].first, m);
    return m[x].first; 
  }
}
    
void unionSet(int x, int y, map<int, pair<int, int>>& m){
  int parX = findSet(x, m);
  int parY = findSet(y, m);
  if(parX == parY) return;
  
  int rankX = m[parX].second; 
  int rankY = m[parY].second;
  if(rankX < rankY) m[parX].first = parY;
  else m[parY].first = parX;
  
  if(rankX == rankY) m[parX].second += 1; 
}

Catalan number

The first Catalan numbers for n = 0, 1, 2, 3, … are

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …

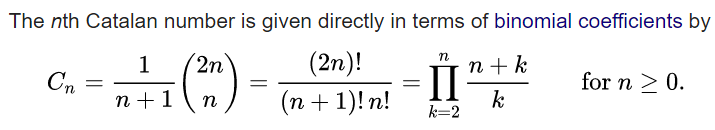
catalan_formula

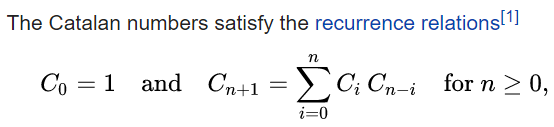
catalan_recursion

Fibonacci number

The first Fibonacci numbers for n = 0, 1, 2, 3, … are

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …

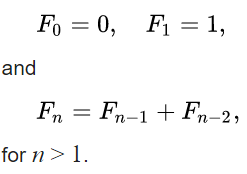
fibonacci_formula

KMP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<vector>
#include<string>

vector<int> buildKmpArray(string& pattern){
  vector<int> kmp(pattern.size() + 1, 0); // temporary array for KMP 
  kmp[0] = -1;
  int j = 0;
  for(int i = 1; i <= pattern.size(); i++){
    kmp[i] = j;
    while(j >= 0 && pattern[j] != pattern[i])
      j = kmp[j];
    j++;
  }
return kmp;
}
    
int KMP(string txt, string pattern) {
  vector<int> kmp = buildKmpArray(pattern);
  // search for pattern
  int j = 0;
  for(int i = 0; i <= txt.size(); i++){
    while(j >= 0 && pattern[j] != txt[i])
      j = kmp[j];
    j++;
    if(j == pattern.size()){
      cout << "match found at " <<  i - pattern.size() + 1 << endl;
      j = kmp[j];
    }
  }
}

1
2
3
4
5
6
7
8
9
10
int binary_search(vector<int>& nums, int target){
  int l = 0, r = nums.size() - 1, m = 0;
  while(l <= r){
    m = l + (r - l) / 2;
    if(nums[m] < target) l = m + 1;
    else if(nums[m] > target) r = m - 1;
    else return m;
  }
  return - 1;
}

argsort in C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <iostream>
#include <vector>
#include <numeric>   // std::iota
#include <algorithm> // std::stable_sort
using namespace std;

vector<int> argsort(vector<int>& v){
  vector<int> idx(v.size());       // idx = {0, 0, 0, ..., 0};
  iota(idx.begin(), idx.end(), 0); // idx = {0, 1, 2, ..., v.size() - 1};
  stable_sort(idx.begin(), idx.end(), [&v](int i1, int i2){return v[i1] < v[i2];});
  return idx;
}

int main(){
  vector<int> v = {23, 40, 10, 15};
  vector<int> idx = argsort(v); 
  for(auto i: idx) cout << i << ", "; // 2, 3, 0, 1, 
}